クソ文系はどこから物理をはじめるの…？
クソ文系（２６歳）は、謙虚です。
基礎の基礎、ド基礎から物理をはじめることにしました。
中学レベルの数学・理科を扱った講座を受講してきました。
学ぶところがたいへんに多かったです（大丈夫か）。
三角比の定義
こちらはお馴染みの三角比の定義です（さすがに知っていました）。
さてこれらを変形してみますと、上記の三式が導かれます。物理ではこちらをよく用いるそうです。
斜辺aを起点にして、底辺b、対辺cを求める恰好の式になっています（ほうほう）。
代表的な三角比は覚えなくてはならないということでした（ここで少し躓きます）。
これがいまいちピンときませんでした。単位円を考えれば、$$sin\theta=y\hspace{8pt}cos\theta=x$$から上記のことは十分導きうるはずなのですが、一体どういう状況なのかイメージが湧きませんでした（このあたりが文系脳）。角度のない三角形にしても、二直角をもつ三角形にしても、クソ文系（２６歳）にはほとんど理解不能でした。ここはあまり難しく考えずに（伝家の宝刀）、数式上の操作（理系っぽい）だけで満足してスルーすることにしました。
連立方程式の着眼点
連立方程式の解法はふたつある（どや）。それは代入法と加減法である（どやどや）。
クソ文系（２６歳）はよくテンパって連立方程式が解けないことはよくありました。とりあえず代入したりして、ぐちゃぐちゃになっておじゃんなんてこともよくありました。果てには未知数と方程式の数が一致していれば、理論的に連立方程式は解けるとか言ってお茶を濁したこともありました（これぞクソ文系）。
まあ、その単純なことなのですが。
解くことができるにしても、解く観点をきちんと意識することが大切であると知りました。
代入するのが適切なのか、それとも加減するのが適切なのか、これまではあまり考えていなかったように振り返ります。
力のつり合い
以上は中学数学でした。ここからは中学理科です。
知らないことだらけ、新しく知ることだらけでした。少し楽しい。
ですが、学習量としてはたいしたことはありません。以下の二点くらいです。
・力を分解して、力の向きをそろえる
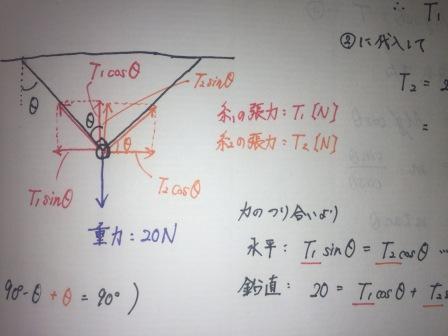
手間取ってしまったことといえば、問題の条件から直角三角形の角度を導くことでした。
この写真でいうと黒のθとオレンジのθです。
錯覚やら90-θなどを駆使（そんなたいそうなことではない）しなくてはなりません。
苦手です。
次はなにをするの？
次回からはようやく高校物理に突入します。
物理基礎という教科ですね。この記事を書いている今もうすでに授業を受け始めています。それだから言えるのですが、ほんとうにこのド基礎講座を受けてよかったということです。そのおかげで初歩で躓くことなく授業についていくことができています。基礎は簡単であるということは意味しませんからね。
ちょっと物理かじったくらいで説教垂れてんじゃねえ
そんな声が聞こえてきそうです。
