受験に熱い高校生や親御さんに限って、偏差値偏差値と熱くなるものですが、「偏差値って何？どうやって求めてるの？」と尋ねると、意外に答えられなくなるものです。 今回は、偏差値の求め方をできるだけ分かりやすく扱うと共に、偏差値を見るときの注意点や、受験生と偏差値の向き合い方についても触れられればと思います。

偏差値って何？

偏差値とは、ある値（例えばテストの点数）が母集団（たとえばクラスのみんなの点数）に対してどれくらいの位置にあるのかを示すもので、高いほど上位にいることが分かります。そして、「50」ならば丁度平均なのが分かります。 さすがにこの辺の話は皆さんもご存知だと思います。では、「偏差値65」とか「偏差値70」とかにはどのような違いがあるのでしょうか。この話に移る前に、さくっと偏差値の求め方を説明しましょう。

偏差値を求めてみよう！

まず、偏差値を出すためには、平均値の出し方と同じく「全部の値」を分かっている必要があります。定期考査で学年全体に対する自分の偏差値を出すためには、学年全員の点数を集める必要があります。だからこそ、試験の偏差値はテストを主催する人（進研模試ならベネッセとか、定期試験なら担当の先生とか）しか求められないのですね。 さて、ここであなたは友達4人の数学の点数を聞き出したものとして、あなたを含む5人の中でのあなたの偏差値を求めてみましょう。

あなた	A君	B君	C君	D君
80点	90点	60点	76点	74点

Step1: まずは平均を求める

偏差値は「自身と平均の差」に重きを置いた指標です。まずは、指標の基軸となる平均値をちゃちゃっと求めましょう。

Step2: 平均の差（偏差）を2乗する

「誰かの点数-平均」を求めて、これを2乗します。5人全員に対してそれぞれ求めてくださいね。 この値は、最後に2乗を伴っているので、必ず0以上の値をとります。そして、良くも悪くも平均から離れているほど（差の大小が極端なほど）大きい値になります。

Step3: 2乗の平均を求める

上で求めた値の平均値をとります。やり方はStep1と同じですね。 ちなみに、この値のことを分散と呼びます。この値が大きいほど、平均値からのデータ全体のかけ離れ具合（データの散らばり具合）が大きいと言えます。

Step4: 2乗の平均の、正の平方根(ルート)を求める

これは電卓必須ゾーンです。上で求めた2乗の平均値(分散)について、正の平方根をとりましょう。 この値のことを標準偏差と呼びます。値が示す意味は分散と同じですが、偏差値を求めるためにはこれを使います。（次元ってものを合わせるためですが、理由を深く考える必要はあまりありません） 標準偏差ならば、模試を受けた1か月後くらいに貰える、集計結果をまとめた冊子に平均点と一緒に掲載されていることがあります。

Step5: 次の式を埋める

点数と平均点の差を標準偏差で割って、これに10を掛け合わせた上で50を加えます。式にすると次の通り。 この式を用いると、あなたの偏差値が次の通り導き出せてめでたしめでたしです。 この式の肝は「（点数ー平均）÷標準偏差」という部分です。「点数ー平均」が大きいほど、この値は大きくなるのですが、標準偏差が大きい（点数が分散している）と小さくなってしまいます。つまり、偏差値は、自分の点数を平均からずば抜けさせると高くなりますし、自分以外のみんなが偶然平均周りの点数をとってくれる（点数がバラけていない）場合も高くなります。 ちなみに、10を掛けて、50を加える部分に数学的な深い意味はありません。10を掛けることによって、値そのものが大きくなります（つまり他の人との差も増えて比較しやすい）し、最後に50を加えることで、平均ぴったりの値を取った人の偏差値が「50」になって、なんとなく分かりやすくなります（0が中心でいいじゃんって人もいると思いますが）。

偏差値が強い時と弱い時

偏差値が強いとき

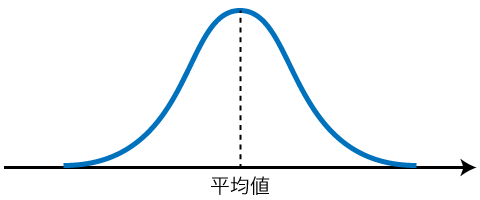
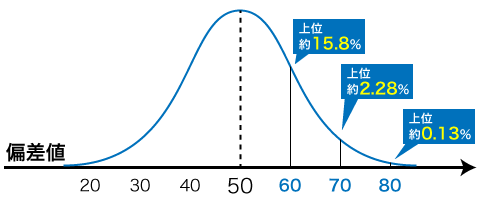
偏差値が大きな役割を果たせるようになるのは、全体の分布が次のような感じになっているときです。 これは「正規分布」と呼ばれる分布の形なのですが、簡単に言えば、「平均に集中していて、平均から離れるほど、個数が少なくなる」「グラフの左右が平均を軸に対称になっている」ような形です。試験で言えば、平均点周りの点数を取る人がもっとも多く、平均から離れるほど、良い点数の人も、はたまた悪い点数の人も同じくらい少なくなるような状況を表します。 このような得点分布をする場合、受験者の「偏差値」は、「上位何%なのか」を的確に表してくれます。 例えば、上のような分布で偏差値70を獲得すると、上位2%くらいに位置しているということができます。逆に、偏差値40を取った人は、左右対称な形から「下位」15.8%くらいの立ち位置にいることが分かります。「偏差値→全体に対する立ち位置」に直接繋がるのは便利ですね。 ちなみに、受験者数が十分に多い模試では、得点の分布が上のグラフの形に近くなることが知られています。したがって、模試の全国偏差値は立ち位置の目安としておおよそ活用できると言えます。

偏差値が弱いとき

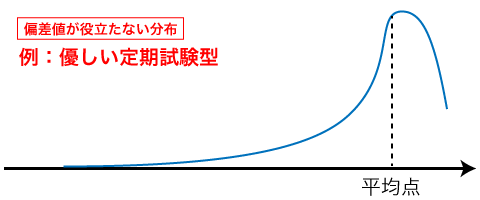
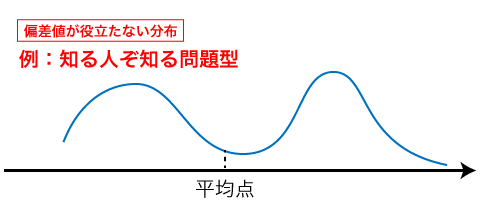
ただし、「偏差値→上位何%なのか」に繋がるのは先ほどのような綺麗な形の分布の場合に限ります。受験者数が圧倒的である全国模試では、大抵このような分布になりますが、例えば、受験者数が少ない場合（集計対象者数が少ない場合）や、問題の難易度設定が不適切な場合、試験の得点分布は必ずしもこんなに上手くいきません。 例えばこんな分布の時は偏差値があまり意味を持ちません。 優しい先生の定期試験にありがちな、やたら平均点が高い例です。「復習すればできる問題」を出題する定期試験では、勉強をした生徒が高得点層に集中し、平均が満点に近づきます。平均点〜満点の間の幅が狭くなり、この幅にたくさんの生徒が集まる一方で、勉強をしない一定の層が相変わらず0点〜平均点の広い幅にまばらに分布するので、グラフが非対称になってしまい、対称なグラフが前提である「偏差値＝上位%」の図式が成り立たなくなります。 これは難しい数学の問題にありがちな例です。数学の問題には、初見では超難しいものの、一度解き方を知ると案外すんなりと解ける例があります。そんな問題がたくさん出題された時、数学の経験が浅い人たちはあっけなく撃沈する一方で、数学を解きまくってる経験豊かな一定層は意外と高得点を獲得しちゃいます。そんな「二極化」が生じた場合、「平均から離れるほどに数が減るグラフ」という前提が崩れて偏差値から母集団の具体的な位置を正しく導けなくなります。

偏差値を扱う上での注意点

以上の説明を踏まえると、偏差値について気をつけるべき点が出てきます。

1.偏差値は、自分の学力だけでなく母集団によっても大きく異なる

偏差値は、ある試験の「自分の点数」と「みんなの点数」だけで導かれる値です。自分の点数が変われば偏差値も変化するのは誰もが知る話なのですが、見落としてはならないことは、偏差値は「みんなの点数」が変わっても変化するため、試験の受験者層が変わった場合に2つの試験の偏差値を安易に比較できない点です。 例えば、進研模試の母集団は幅広い学力層を抱えている一方で、駿台ハイレベル模試は、難関大志望者ばかりが受験します。前者の集団では良い立ち位置にいたとしても、後者では悪い位置に立つことなんてザラですので、2つの試験を受けたとき、自分の学力が同じでも、前者の偏差値は高く出て、後者の偏差値は（とても）低く出ることがよくあります。偏差値だけでは自分の学力と周りの学力のどちらが変わったのか分からないので、自分の学力を示す普遍的な指標として偏差値を見るのはNGです！

2.偏差値は必ずしも有用な意味を持たない

偏差値は得点の分布によって有用性が大きく変わります。例えば、定期考査のようなそもそもの受験者が少ない試験や、全国模試の校内偏差値のような「集計対象者」が少ない試験では、分布の形状に歪みが生じてしまい、偏差値が大きな意味を持たなくなることがあります。 定期考査で偏差値が出ることはほとんどないと思いますが、全国模試の校内偏差値などはあまり深く捉えず、軽く眺める程度に留めておくと良いでしょう。

3.大学は偏差値のみで測れない

受験界には「偏差値表」なる表があります。これを大学の格付けや順位付けの材料として扱うことが的外れなのは、偏差値表の意味から明らかなのですが、なぜかそのことを理解している高校生はそう多くありません。 そもそも、予備校が作成する「偏差値表」は、ある人が過去に受けた模試の全国偏差値と実際の入試結果を紐付けして作成されるもので、「この模試でこれ位の偏差値を取っていると、だいたいこれ位の確率でこの大学に受かりますよ」という目安にすぎません。よって、偏差値表が示すのは、大学に入る難しさのみであり、大学に入ってからの教育の充実度や研究の規模や貢献度、校風やサークル活動の活発度など、本来大学選びにおいて重要となる要素は偏差値からほとんど読み取れない点に注意が必要です（「全く」ではなく「ほとんど」としたのは、入試で求められる学力と大学の魅力に相関が一切見られないとも断言できないからです）。偏差値表で大学を評価しているうちはまだまだ大学選び初心者ですよ。

さいごに

この記事では、偏差値の求め方と偏差値を扱う上での注意点について述べました。 偏差値は、全体に対する自分の立ち位置が具体的な数値として表れる点、入試に臨む中で大学の入学難度と自身の学力との距離を簡単に測れる点で便利ですが、全体となる母集団や、試験のタイプなどに留意して、この数字に囚われすぎることのないようにしましょうね。